Energize Two-Level Factorials - Add Center Points!

Two-level factorial designs are highly effective for discovering active factors and interactions in a process, and are optimal for fitting linear models by simply comparing low vs high factor settings. Super-charge these classic designs by adding center points!
(Read to the end for a bonus video clip!)

There is an underlying assumption that the straight-line model also fits the interior of the design space, but there is no actual check on this assumption unless center points (the mid-level) are added to the design. Figure 1 illustrates how the addition of center points helps you detect non-linearity in the middle of the experimental space.

A center point is located at the exact mid-point of all factor settings. The example in Figure 2 shows a cookie baking experiment where the center point is replicated four times at the mid-point of 10 minutes and 350 degrees.

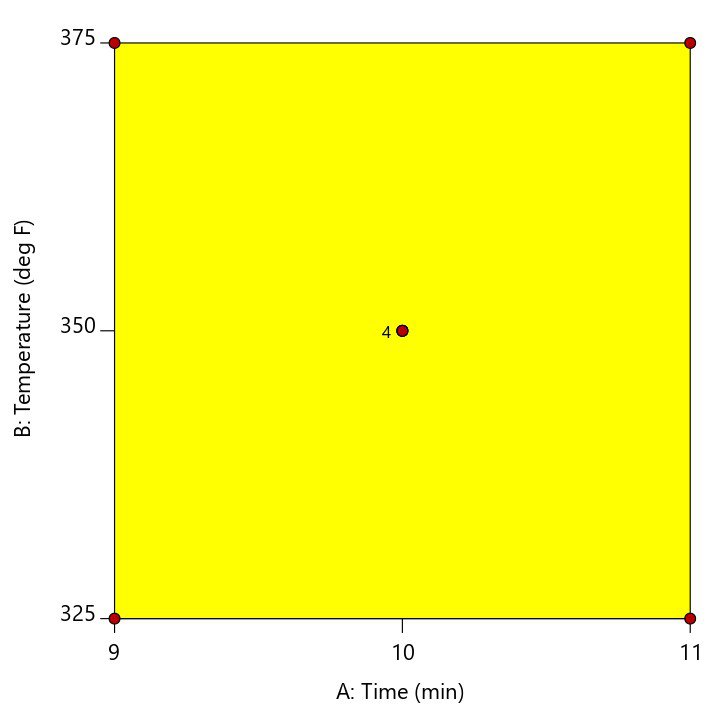
Multiple center points (replicates) should be randomized throughout the other experimental conditions to get an adequate assessment of whether the actual values measured at this point match what is predicted by the linear model. This is called a test for curvature. If the curvature test is significant, this is considered evidence that a quadratic or higher order model is required to model the relationship between the factors and the response. If the curvature test is not significant, then it is okay to assume that the linear model fits in the middle of the design space.

In Design-Expert® software, version 11, the curvature test is placed in front of the ANOVA when you have included center points in the design. This immediately shows you if the model is significant, and if the curvature is significant. As illustrated by the screen shot below (Figure 3), advice is provided to guide your next steps.

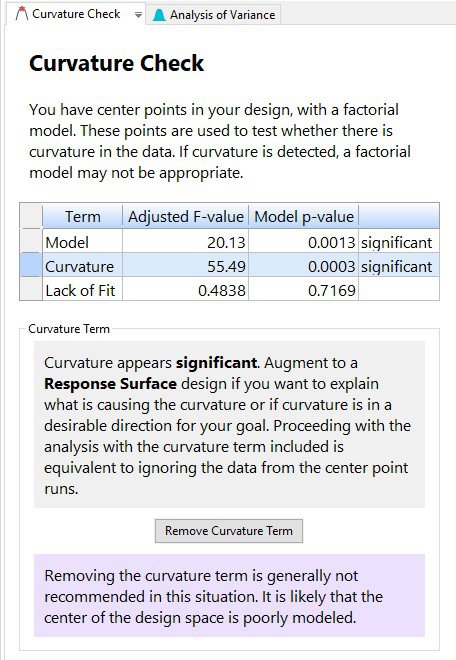
New to DX11, is the “Remove Curvature Term” button. If curvature is significant and you click on this button, then the regression modeling is done by using all the data, including the center points. Because the actual center points are not sitting in the middle of the design space, it is highly likely that the resulting model will be poorly fit and the lack of fit statistic will be significant. Then, click on “Add Curvature Term” to put the curvature effect back into the model, thus accounting for the information in the middle of the design space.

Ultimately, if curvature is significant, the recommendation is to augment the design to a response surface design to better model the relationship between the factors and the response. If curvature is NOT significant, then proceeding with the analysis is acceptable.

For further details on curvature, check out the DOE Simplified textbook, or enroll in an upcoming Modern DOE for Process Optimization workshop.

Bonus: Check out Mark’s 1-minute video on this topic: MiniTip 2 - Center points in factorials