The Importance of Center Points in Central Composite Designs
A central composite design (CCD) is a type of response surface design that will give you very good predictions in the middle of the design space. Many people ask how many center points (CPs) they need to put into a CCD. The number of CPs chosen (typically 5 or 6) influences how the design functions.
Two things need to be considered when choosing the number of CPs in a central composite design:
1) Replicated center points are used to estimate pure error for the lack of fit test. Lack of fit indicates how well the model you have chosen fits the data. With fewer than five or six replicates, the lack of fit test has very low power. You can compare the critical F-values (with a 5% risk level) for a three-factor CCD with 6 center points, versus a design with 3 center points. The 6 center point design will require a critical F-value for lack of fit of 5.05, while the 3 center point design uses a critical F-value of 19.30. This means that the design with only 3 center points is less likely to show a significant lack of fit, even if it is there, making the test almost meaningless.
TIP: True “replicates” are runs that are performed at random intervals during the experiment. It is very important that they capture the true normal process variation! Do not run all the center points grouped together as then most likely their variation will underestimate the real process variation.
2) The default number of center points provides near uniform precision designs. This means that the prediction error inside a sphere that has a radius equal to the ±1 levels is nearly uniform. Thus, your predictions in this region (±1) are equally good. Too few center points inflate the error in the region you are most interested in. This effect (a “bump” in the middle of the graph) can be seen by viewing the standard error plot, as shown in Figures 1 & 2 below. (To see this graph, click on Design Evaluation, Graph and then View, 3D Surface after setting up a design.)

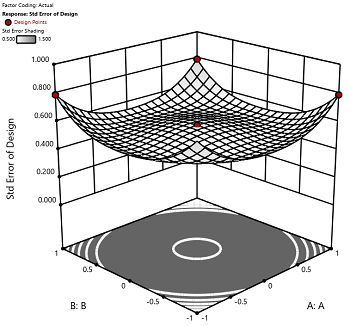
Figure 1 (left): CCD with the 6 center points (5-6 recommended). Figure 2 (right): CCD with only 3 center points. Notice the jump in standard error at the center of figure 2.
Ask yourself this—where do you want the best predictions? Most likely at the middle of the design space. Reducing the number of center points away from the default will substantially damage the prediction capability here! Although it can seem tedious to run all of these replicates, the number of center points does ensure that the analysis of the design can be done well, and that the design is statistically sound.
