Stat-Ease Blog

Categories
Tips and tricks for designing statistically optimal experiments
Like the blog? Never miss a post - sign up for our blog post mailing list.
A fellow chemical engineer recently asked our StatHelp team about setting up a response surface method (RSM) process optimization aimed at establishing the boundaries of his system and finding the peak of performance. He had been going with the Stat-Ease software default of I-optimality for custom RSM designs. However, it seemed to him that this optimality “focuses more on the extremes” than modified distance or distance.
My short answer, published in our September-October 2025 DOE FAQ Alert, is that I do not completely agree that I-optimality tends to be too extreme. It actually does a lot better at putting points in the interior than D-optimality as shown in Figure 2 of "Practical Aspects for Designing Statistically Optimal Experiments." For that reason, Stat-Ease software defaults to I-optimal design for optimization and D-optimal for screening (process factorials or extreme-vertices mixture).
I also advised this engineer to keep in mind that, if users go along with the I-optimality recommended for custom RSM designs and keep the 5 lack-of-fit points added by default using a distance-based algorithm, they achieve an outstanding combination of ideally located model points plus other points that fill in the gaps.
For a more comprehensive answer, I will now illustrate via a simple two-factor case how the choice of optimality parameters in Stat-Ease software affects the layout of design points. I will finish up with a tip for creating custom RSM designs that may be more practical than ones created by the software strictly based on optimality.
An illustrative case
To explore options for optimal design, I rebuilt the two-factor multilinearly constrained “Reactive Extrusion” data provided via Stat-Ease program Help to accompany the software’s Optimal Design tutorial via three options for the criteria: I vs D vs modified distance. (Stat-Ease software offers other options, but these three provided a good array to address the user’s question.)
For my first round of designs, I specified coordinate exchange for point selection aimed at fitting a quadratic model. (The default option tries both coordinate and point exchange. Coordinate exchange usually wins out, but not always due to the random seed in the selection algorithm. I did not want to take that chance.)
As shown in Figure 1, I added 3 additional model points for increased precision and kept the default numbers of 5 each for the lack-of-fit and replicate points.
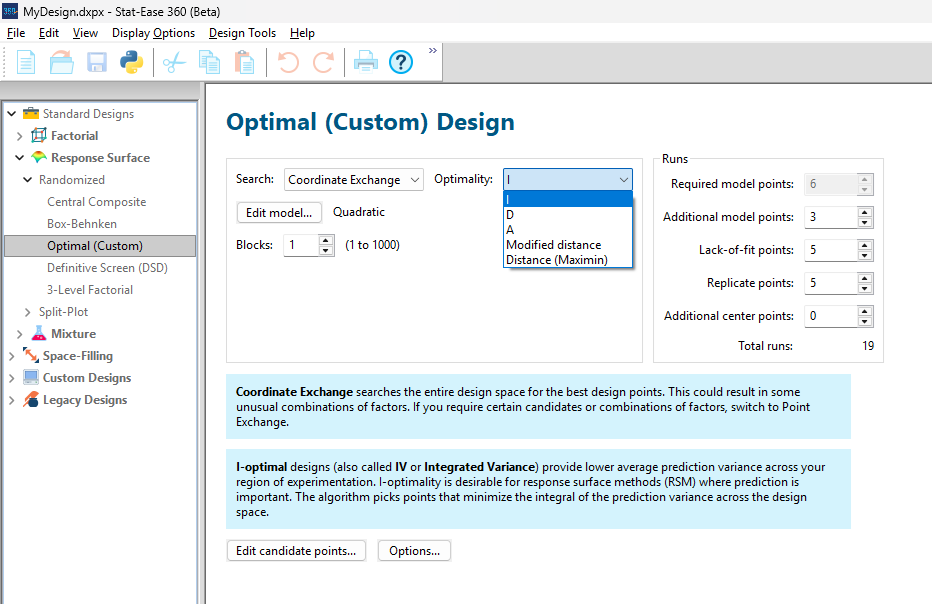
Figure 1: Set up for three alternative designs—I (default) versus D versus modified distance
As seen in Figure 2’s contour graphs produced by Stat-Ease software’s design evaluation tools for assessing standard error throughout the experimental region, the differences in point location are trivial for only two factors. (Replicated points display the number 2 next to their location.)
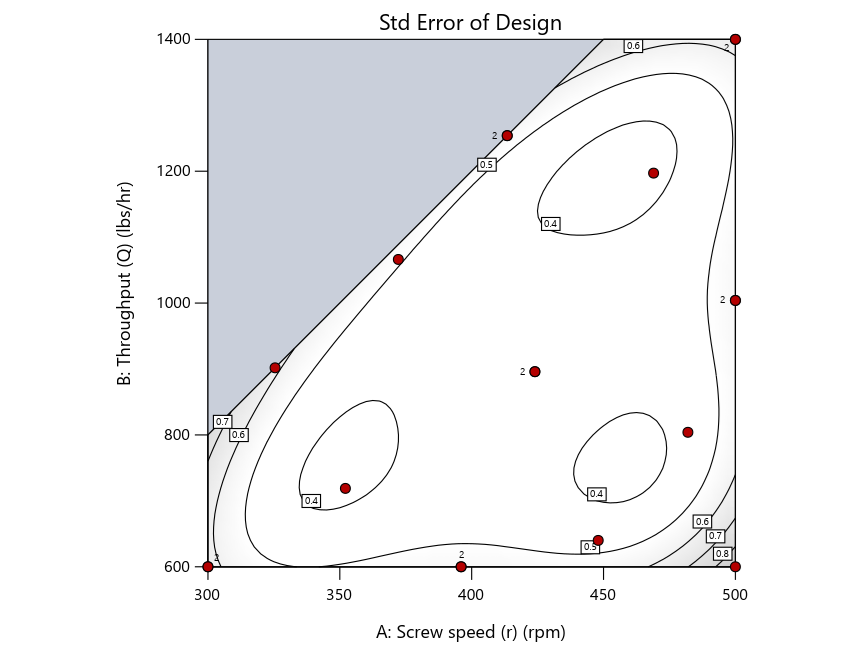
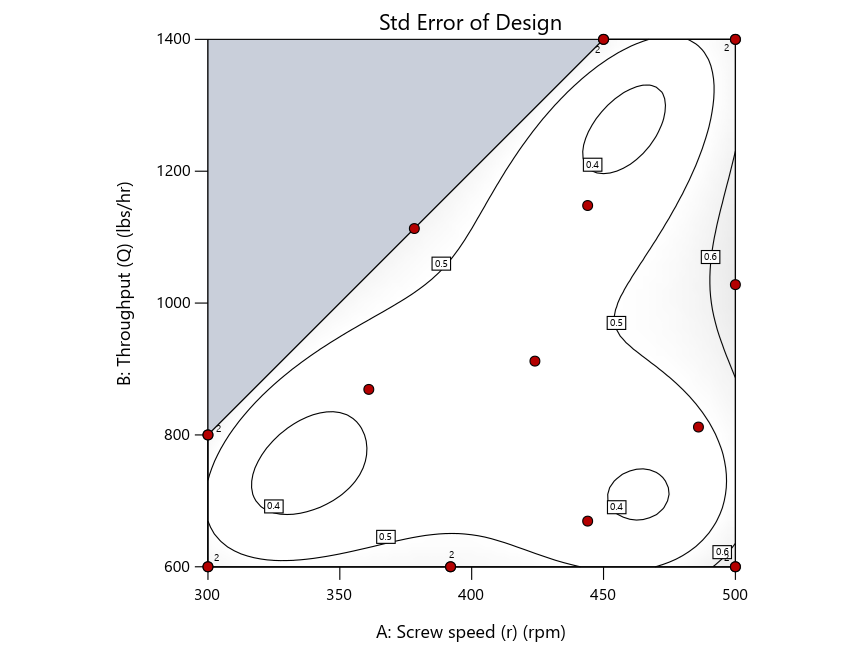
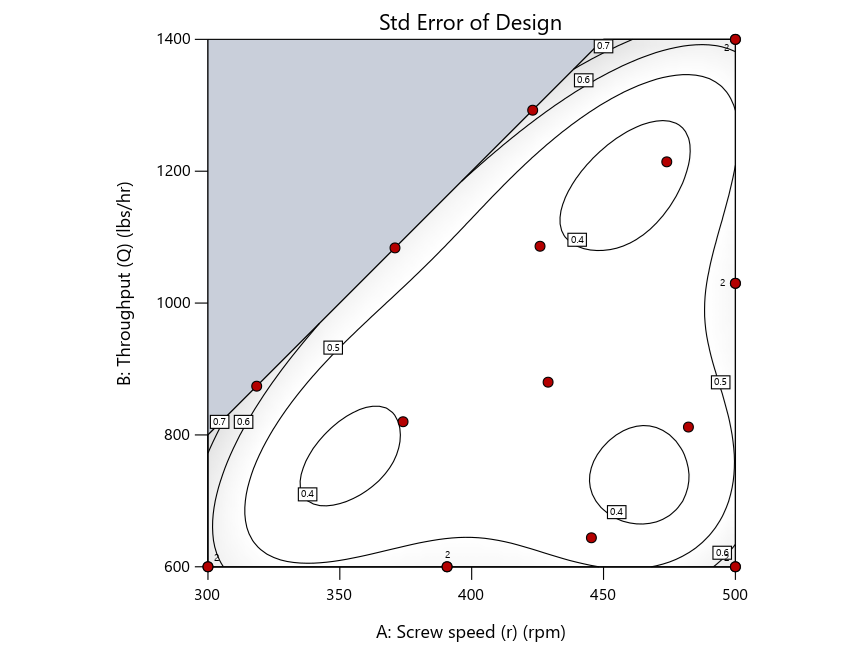
Figure 2: Designs built by I vs D vs modified distance including 5 lack-of-fit points (left to right)
Keeping in mind that, due to the random seed in our algorithm, run-settings vary when rebuilding designs, I removed the lack-of-fit points (and replicates) to create the graphs in Figure 2.
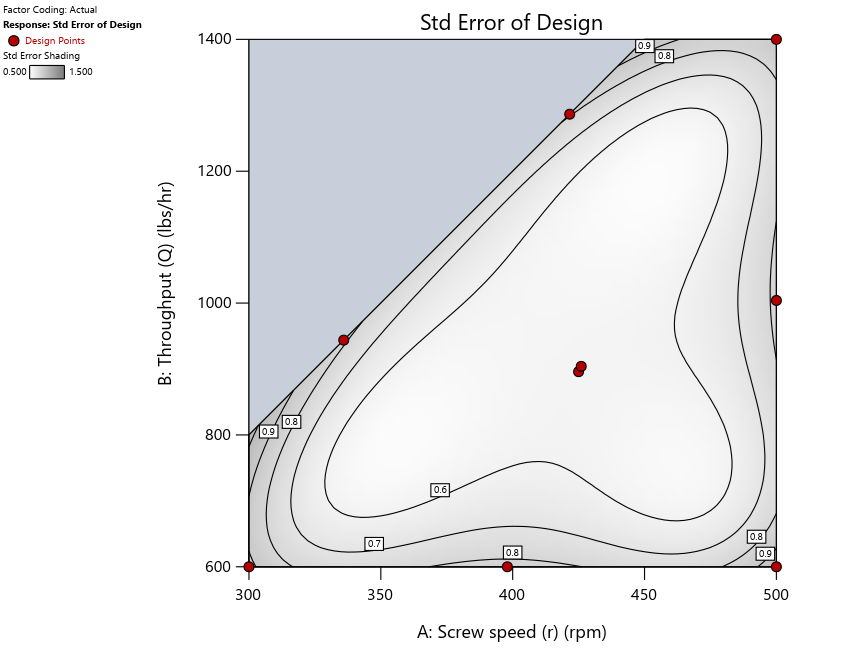
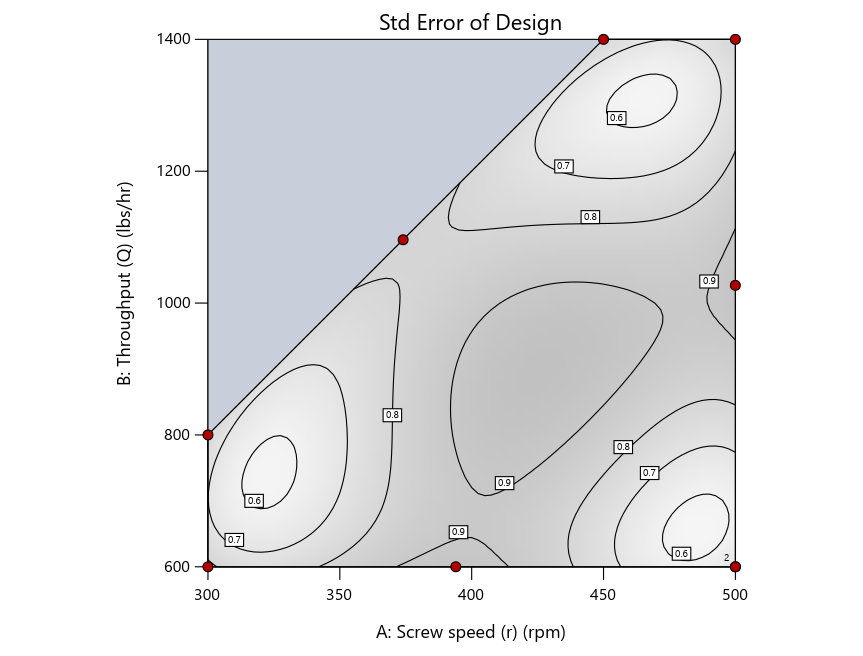
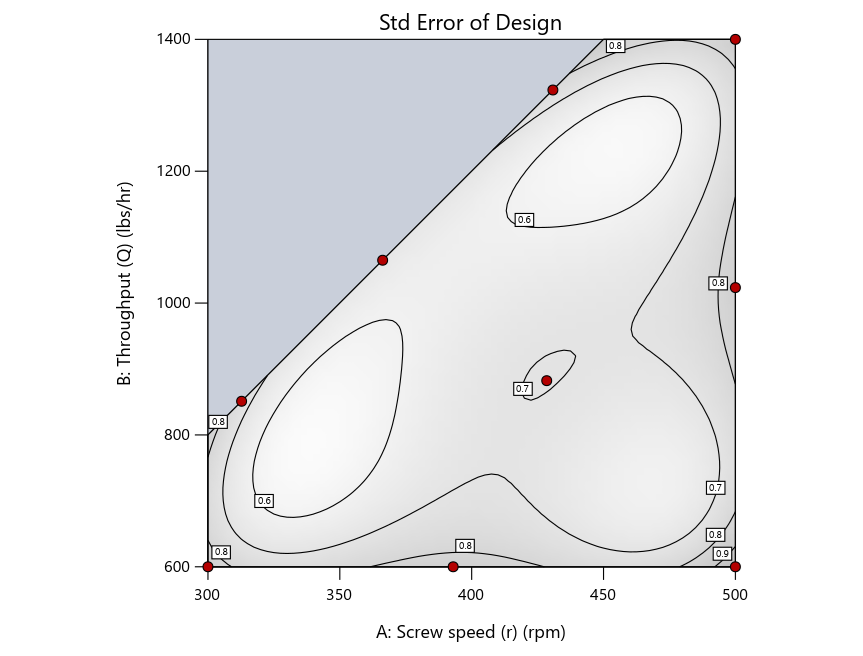
Figure 3: Designs built by I vs D vs modified distance excluding lack-of-fit points (left to right)
Now you can see that D-optimal designs put points around the outside, whereas I-optimal designs put points in the interior, and the space-filling criterion spreads the points around. Due to the lack of points in the interior, the D-optimal design in this scenario features a big increase in standard error as seen by the darker shading—a very helpful graphical feature in Stat-Ease software. It is the loser as a criterion for a custom RSM design. The I-optimal wins by providing the lowest standard error throughout the interior as indicated by the light shading. Modified distance base selection comes close to I optimal but comes up a bit short—I award it second place, but it would not bother me if a user liking a better spread of their design points make it their choice.
In conclusion, as I advised in my DOE FAQ Alert, to keep things simple, accept the Stat-Ease software custom-design defaults of I optimality with 5 lack-of-fit points included and 5 replicate points. If you need more precision, add extra model points. If the default design is too big, cut back to 3 lack-of-fit points included and 3 replicate points. When in a desperate situation requiring an absolute minimum of runs, zero out the optional points and ignore the warning that Stat-Ease software pops up (a practice that I do not generally recommend!).
A practical tip for point selection
Look closely at the I-optimal design created by coordinate exchange in Figure 3 on the left and notice that two points are placed in nearly the same location (you may need a magnifying glass to see the offset!). To avoid nonsensical run specifications like this, I prefer to force the exchange algorithm to point selection. This restricts design points to a geometrically registered candidate set, that is, the points cannot move freely to any location in the experimental region as allowed by coordinate exchange.
Figure 4 shows the location of runs for the reactive-extrusion experiment with point selection specified.
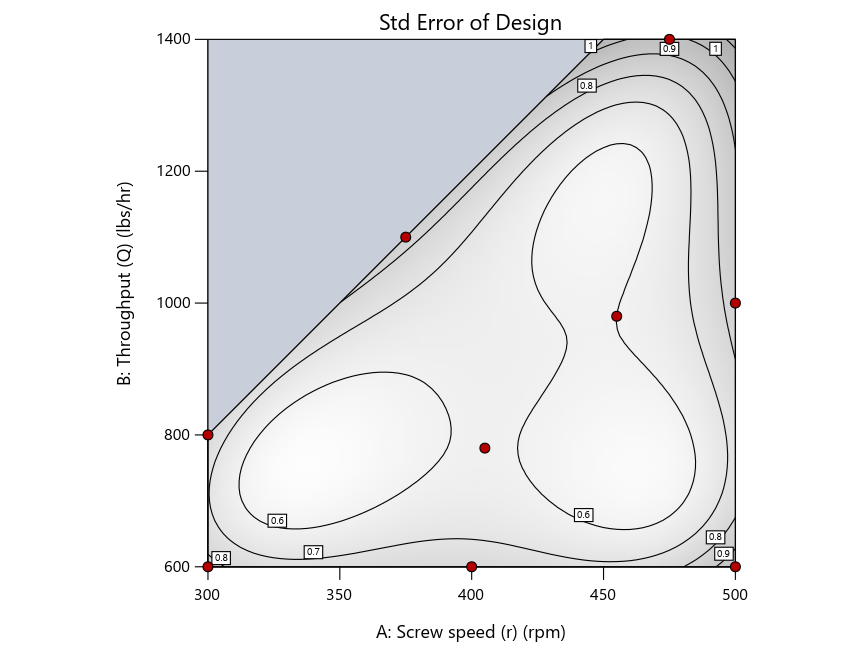
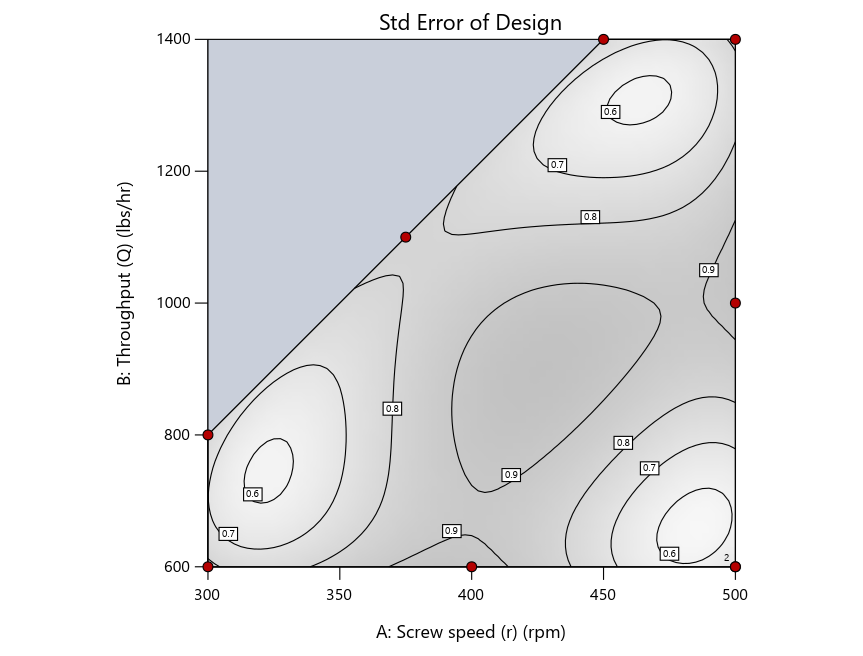
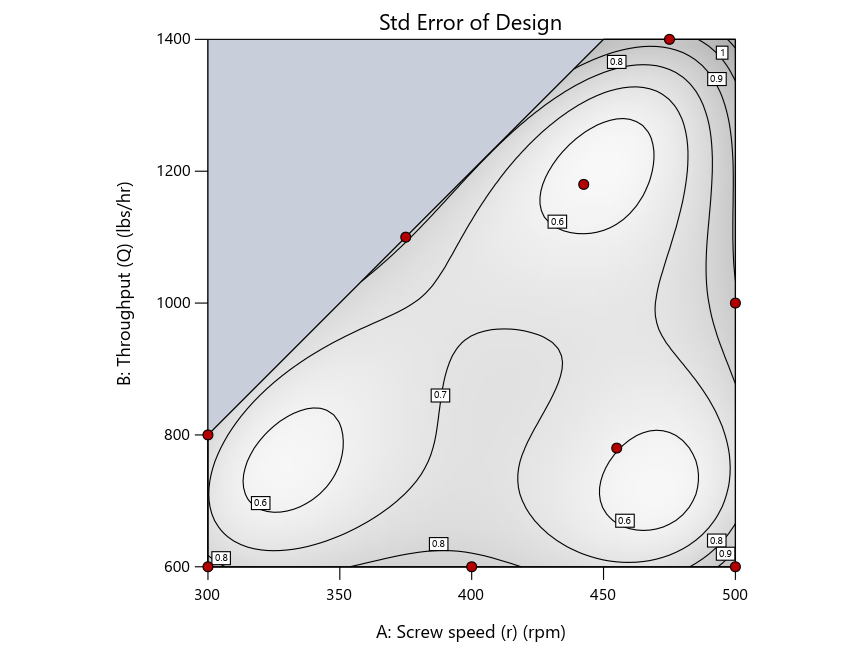
Figure 4: Designs built by I vs D vs modified distance by point exchange (left to right)
The D optimal remains a bad choice—the same as before. The edge for I optimal over modified distance narrows due to point exchange not performing quite as well for as coordinate exchange.
As an engineer with a wealth of experience doing process development, I like the point exchange because it:
- Reaches out for the ‘corners’—the vertices in the design space,
- Restricts runs to specific locations, and
- Allows users to see where they are by showing space point type on the design layout enabled via a right-click over the upper left corner.
Figures 5a and 5b illustrate this advantage of point over coordinate exchange.
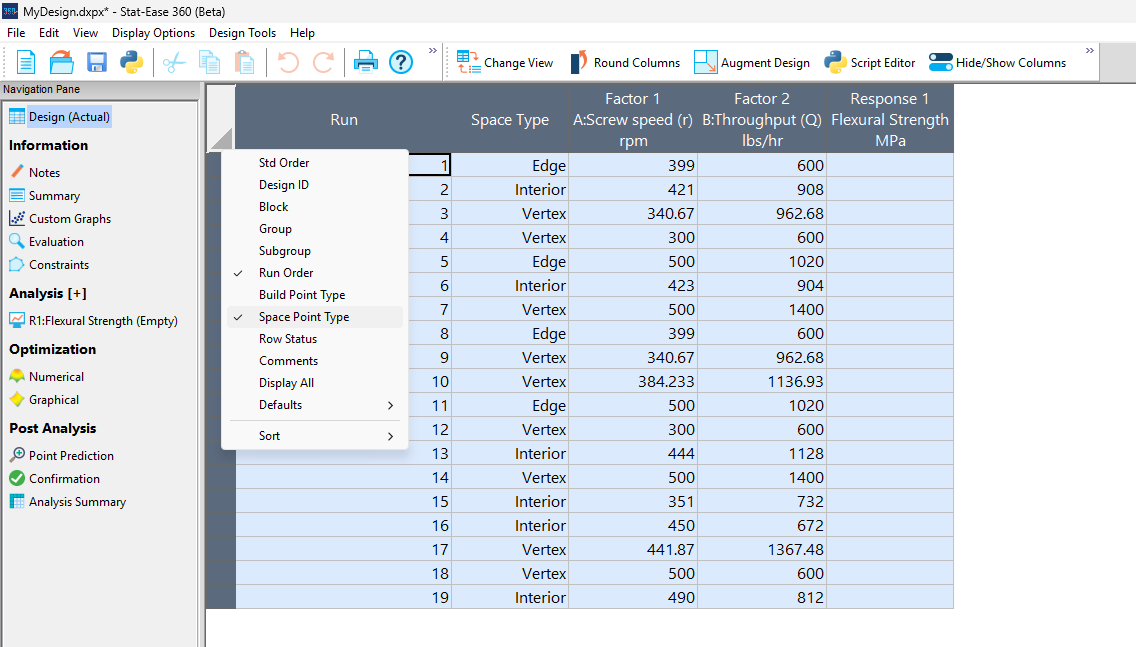
Figure 5a: Design built by coordinate exchange with Space Point Type toggled on
On the table displayed in Figure 5a for a design built by coordinate exchange, notice how points are identified as “Vertex” (good the software recognized this!), “Edge” (not very specific) and “Interior” (only somewhat helpful).
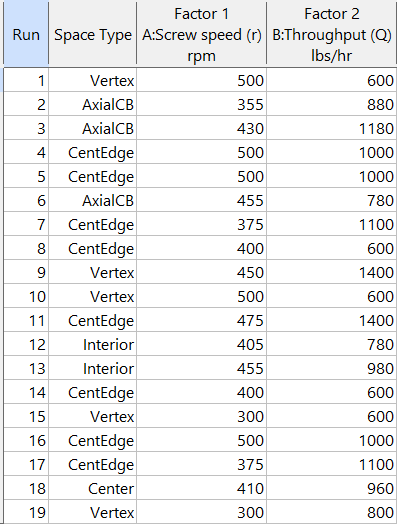
Figure 5b: Design built by point exchange with Space Point Type shown
As shown by Figure 5b, rebuilding the design via point exchange produces more meaningful identification of locations (and better registered geometrically): “Vertex” (a corner), “CentEdge” (center of edge—a good place to make a run), “Center” (another logical selection) and “Interior” (best bring up the contour graph via design evaluation to work out where these are located—click any point to identify them by run number).
Full disclosure: There is a downside to point exchange—as the number of factors increases beyond 12, the candidate set becomes excessive and thus the build takes more time than you may be willing to accept. Therefore, Stat-Ease software recommends going only with the far faster coordinate exchange. If you override this suggestion and persist with point exchange, no worries—during the build you can cancel it and switch to coordinate exchange.
Final words
A fellow chemical engineer often chastised me by saying “Mark, you are overthinking things again.” Sorry about that. If you prefer to keep things simple (and keep statisticians happy!), go with the Stat-Ease software defaults for optimal designs. Allow it to run both exchanges and choose the most optimal one, even though this will likely be the coordinate exchange. Then use the handy Round Columns tool (seen atop Figure 5a) to reduce the number of decimal places on impossibly precise settings.
Like the blog? Never miss a post - sign up for our blog post mailing list.
August Publication Roundup
Here's the latest Publication Roundup! In these monthly posts, we'll feature recent papers that cited Design-Expert® or Stat-Ease® 360 software. Please submit your paper to us if you haven't seen it featured yet!
Featured Article
Design and optimization of imageable microspheres for locoregional cancer therapy
Scientific Reports volume 15, Article number: 27487 (2025)
Authors: Brenna Kettlewell, Andrea Armstrong, Kirill Levin, Riad Salem, Edward Kim, Robert J. Lewandowski, Alexander Loizides, Robert J. Abraham, Daniel Boyd
Mark's comments: This is a great application of mixture design for optimal formulation of a medical-grade glass. The researchers used Stat-Ease software tools to improve the properties of microspheres to an extent that their use can be extended to cancers beyond the current application to those located in the liver. Well done!
Be sure to check out this important study, and the other research listed below!
More new publications from August
- Use of experimental design for screening and optimization of variables influencing photocatalytic degradation of pollutants in aqueous media: A review of chemometrics tools
Chemical Engineering Research and Design, Volume 220, August 2025, Pages 270-291
Authors: Pedro César Quero–Jiménez, Aracely Hernández–Ramírez, Jorge Luis Guzmán–Mar, Jorge Basilio de la Torre–López, Matheus Silva–Gigante, Laura Hinojosa–Reyes - Analytical Quality by Design-Based Stability-Indicating UHPLC Method for Determination of Inavolisib in Bulk and Formulation
Separation Science Plus, no. 8 (2025): 8, e70110
Authors: Ashwinkumar Matta, Raja Sundararajan - Enhanced anti-infective activities of sinapic acid through nebulization of lyophilized protransferosomes
Frontiers in Nanotechnology | Biomedical Nanotechnology, Volume 7 - 2025
Authors: Hani A. Alhadrami, Amr Gamal, Ngozi Amaeze, Ahmed M. Sayed, Mostafa E. Rateb, and Demiana M. Naguib - Optimizing Anti-Corrosive Properties of Polyester Powder Coatings Through Montmorillonite-Based Nanoclay Additive and Film Thickness
Corrosion and Materials Degradation, 2025, 6(3), 39
Authors: Marshall Shuai Yang, Chengqian Xian, Jian Chen, Yolanda Susanne Hedberg, James Joseph Noël - Regulatory mechanism and multi-index coordinated optimization of pipeline transportation performance of coarse-grained gangue slurry: Experimental and simulation investigation
Physics of Fluids 37, 073343 (2025)
Authors: Jianfei Xu (许健飞); Jixiong Zhang (张吉雄); Nan Zhou (周楠); Hao Yan (闫浩); Wenfu Zhou (周文福); Qian Chen (陈乾); Jiarun Chen (陈嘉润) - Optimization of clayey soil parameters with aeolian sand through response surface methodology and a desirability function
Scientific Reports volume 15, Article number: 30831 (2025)
Authors: Ghania Boukhatem, Messaouda Bencheikh, Mohammed Benzerara, Mehmet Serkan Kırgız, N. Nagaprasad, Krishnaraj Ramaswamy, Souhila Rehab-Bekkouche, R. Shanmugam - Development of electromagnetic drop weight release mechanism for human occupied vehicle
Scientific Reports volume 15, Article number: 30663 (2025)
Authors: Sathia Narayanan Dharmaraj, Karthikeyan Shanmugam, Jothi Chithiravel, Ramesh Sethuraman - Operating parameter optimization and experiment of spiral outer grooved wheel seed metering device based on discrete element method
Scientific Reports volume 15, Article number: 30762 (2025)
Authors: Tao Zhang, Xinglong Tang, Cong Dai, Guiying Ren - Parameter optimization of key components in seed-metering device for pre-cut seed stems of Pennisetum hydridum
Scientific Reports volume 15, Article number: 31318 (2025)
Authors: Chong Liu, Xiongfei Chen, Qiang Xiong, Muhua Liu, Junan Liu, Jiajia Yu, Peng Fang, Yihan Zhou, Chuanhong Zhan, Yao Xiao - Optimization of new and thermally aged natural monoesters blends for a sustainable management of power transformers
Industrial Crops and Products, Volume 235, 1 November 2025, 121741
Authors: Gerard Ombick Boyekong, Gabriel Ekemb, Emeric Tchamdjio Nkouetcha, Ghislain Mengata Mengounou, Adolphe Moukengue Imano
Perfecting pound cake via mixture design for optimal formulation
Thanksgiving is fast approaching—time to begin the meal planning. With this in mind, the NBC Today show’s October 22nd tips for "75 Thanksgiving desserts for the sweetest end to your feast" caught my eye, in particular the Donut Loaf pound cake. My 11 grandkids would love this “giant powdered sugar donut” (and their Poppa, too!).
I became a big fan of pound cake in the early 1990s while teaching DOE to food scientists at Sara Lee Corporation. Their ready-made pound cakes really hit the spot. However, it is hard to beat starting from scratch and baking your own pound cake. The recipe goes backs hundreds of years to a time when many people could not read, thus it simply called for a pound each of flour, butter, sugar and eggs. Not having a strong interest in baking and wanting to minimize ingredients and complexity (other than adding milk for moisture and baking powder for tenderness), I made this formulation my starting point for a mixture DOE, using the Sara Lee classic pound cake as the standard for comparison.
As I always advise Stat-Ease clients, before designing an experiment, begin with the first principles. I took advantage of my work with Sara Lee to gain insights on the food science of pound cake. Then I checked out Rose Levy Beranbaum’s The Cake Bible from my local library. I was a bit dismayed to learn from this research that the experts recommended cake flour, which costs about four times more than the all-purpose (AP) variety. Having worked in a flour mill during my time at General Mills as a process engineer, I was skeptical. Therefore, I developed a way to ‘have my cake and eat it too’: via a multicomponent constraint (MCC), my experiment design incorporated both varieties of flour. Figure 1 shows how to enter this in Stat-Ease software.

Figure 1. Setting up the pound cake experiment with a multicomponent constraint on the flours
By the way, as you can see in the screen shot, I scaled back the total weight of each experimental cake to 1 pound (16 ounces by weight), keeping each of the four ingredients in a specified range with the MCC preventing the combined amount of flour from going out of bounds.
The trace plot shown in Figure 2 provides the ingredient directions for a pound cake that pleases kids (based on tastes of my young family of 5 at the time) are straight-forward: more sugar, less eggs and go with the cheap AP flour (its track not appreciably different than the cake flour.)

Figure 2. Trace plot for pound cake experiment
For all the details on my pound cake experiment, refer to "Mixing it up with Computer-Aided Design"—the manuscript for a publication by Today's Chemist at Work in their November 1997 issue. This DOE is also featured in “MCCs Made as Easy as Making a Pound Cake” in Chapter 6 of Formulation Simplified: Finding the Sweet Spot through Design and Analysis of Experiments with Mixtures.
The only thing I would do different nowadays is pour a lot of powdered sugar over the top a la the Today show recipe. One thing that I will not do, despite it being so popular during the Halloween/Thanksgiving season, is add pumpkin spice. But go ahead if you like—do your own thing while experimenting on pound cake for your family’s feast. Happy holidays! Enjoy!
To learn more about MCCs and master DOE for food, chemical, pharmaceutical, cosmetic or any other recipe improvement projects, enroll in a Stat-Ease “Mixture Design for Optimal Formulations” public workshop or arrange for a private presentation to your R&D team.
Strategy of Experiments for Formulations: Try Screening First!
Consider Screening Down Components to a Vital Few Before Studying Them In-Depth
At the outset of my chemical engineering career, I spent 2 years working with various R&D groups for a petroleum company in Southern California. One of my rotations brought me to their tertiary oil-recovery lab, which featured a wall of shelves filled to the brim with hundreds of surfactants. It amazed me how the chemist would seemingly know just the right combination of anionic, nonionic, cationic and amphoteric varieties to blend for the desired performance. I often wondered, though, whether empirical screening might have paid off by revealing a few surprisingly better ingredients. Then after settling in on the vital few components doing an in-depth experiment may very well have led to discovery of previously unknown synergisms. However, this was before the advent of personal computers and software for mixture design of experiments (DOE), and, thus, extremely daunting for non-statisticians.
Nowadays I help many formulators make the most from mixture DOE via Stat-Ease softwares’ easy-to-use statistical tools. I was very encouraged to see this 2021 meta-analysis that found 200 or so recent publications (2016-2020) demonstrating the successful application of mixture DOE for food, beverage and pharmaceutical formulation development. I believe that this number can be multiplied many-fold to extrapolate these findings to other process industries—chemicals, coatings, cosmetics, plastics, and so forth. Also, keep in mind that most successes never get published—kept confidential until patented.
However, though I am very heartened by the widespread adoption of mixture DOE, screening remains underutilized based on my experience and a very meager yield of publications from 2016 to present from a Google-Scholar search. I believe the main reasons to be:
- Formulators prefer to rely on their profound knowledge of the chemistry for selection of ingredients (refer to my story about surfactants for tertiary oil recovery)
- The number of possibilities get overwhelming; for example, this 2016 Nature publication reports that experimenters on a pear cell suspension culture got thrown off by the 65 blends they believed were required for simplex screening of 20 components (too bad, as shown in the Stat-Ease software screenshot below, by cutting out the optional check blends and constraint-plane-centroids, this could be cut back to substantially.)

- Misapplying factorial screening to mixtures, which, unfortunately happens a lot due to these process-focused experiments being simpler and more commonly used. This is really a shame as pointed out in this Stat-Ease blog post
I feel sure that it pays to screen down many components to a vital few before doing an in-depth optimization study. Stat-Ease software provides some great options for doing so. Give screening a try!!
For more details on mixture screening designs and a solid strategy of experiments for optimizing formulations, see my webinar on Strategy of Experiments for Optimal Formulation. If you would like to speak with our team about putting mixture DOE to good use for your R&D, please contact us.
Wrap-Up: Thanks for a great 2022 Online DOE Summit!
Thank you to our presenters and all the attendees who showed up to our 2022 Online DOE Summit! We're proud to host this annual, premier DOE conference to help connect practitioners of design of experiments and spread best practices & tips throughout the global research community. Nearly 300 scientists from around the world were able to make it to the live sessions, and many more will be able to view the recordings on the Stat-Ease YouTube channel in the coming months.
Due to a scheduling conflict, we had to move Martin Bezener's talk on "The Latest and Greatest in Design-Expert and Stat-Ease 360." This presentation will provide a briefing on the major innovations now available with our advanced software product, Stat-Ease 360, and a bit of what's in store for the future. Attend the whole talk to be entered into a drawing for a free copy of the book DOE Simplified: Practical Tools for Effective Experimentation, 3rd Edition. New date and time: Wednesday, October 12, 2022 at 10 am US Central time.
Even if you registered for the Summit already, you'll need to register for the new time on October 12. Click this link to head to the registration page. If you are not able to attend the live session, go to the Stat-Ease YouTube channel for the recording.

Want to be notified about our upcoming live webinars throughout the year, or about other educational opportunities? Think you'll be ready to speak on your own DOE experiences next year? Sign up for our mailing list! We send emails every month to let you know what's happening at Stat-Ease. If you just want the highlights, sign up for the DOE FAQ Alert to receive a newsletter from Engineering Consultant Mark Anderson every other month.
Thank you again for helping to make the 2022 Online DOE Summit a huge success, and we'll see you again in 2023!
